物以类聚,人以群分。在机器学习中,对于海量的数据,经常要做的一件事就是找出他们之间的特征,将这些数据归类,就像德米特里·门捷列夫一样把各个元素整齐的排在一起,后面形成了元素周期表。
在行业中这个做法有个专业的名词叫“聚类/分类”,今天要和大家一起分享的是聚类中最常见的算法:K-Means 算法。
前言
在开始之前,必须也必要让大家知道“监督式学习”和“非监督式学习”的区别,因为这个概念非常重要,只有根深蒂固的记在脑海里,对于学习机器学习有很大的帮助,思维模式也不一样。
监督式学习:输入的数据有标签。
非监督式学习:输入的数据没有标签。
K-Means 算法属于非监督式
在非监督式学习中,聚类任务是使用最多的,而 K-Means 算法是聚类任务中最简单、最好理解、运算最快的一种算法。聚类的主要思想就是物以类聚,人以群分,在 K-Means 算法中实现起来主要分以下几个步骤:
- 定义一个 k 值,这个 k 决定了聚类后有几个类别
- 从数据中随机选出 k 个数据点做为初始研究对象
- 然后把剩下的数据点当作投票者,投给谁,自己以后就跟谁。他们投票的方式是计算自己与已确定的研究对象的距离,谁和自己距离小,就投给谁
- 第一轮投票完成,为了公平,重复投票,这次的初始对象就不是随便选,而是在已投票的 k 堆中选取
- 重复上面的步骤,直到和预期的一致
实例
为了方便说明,我模拟一组数据,如下图
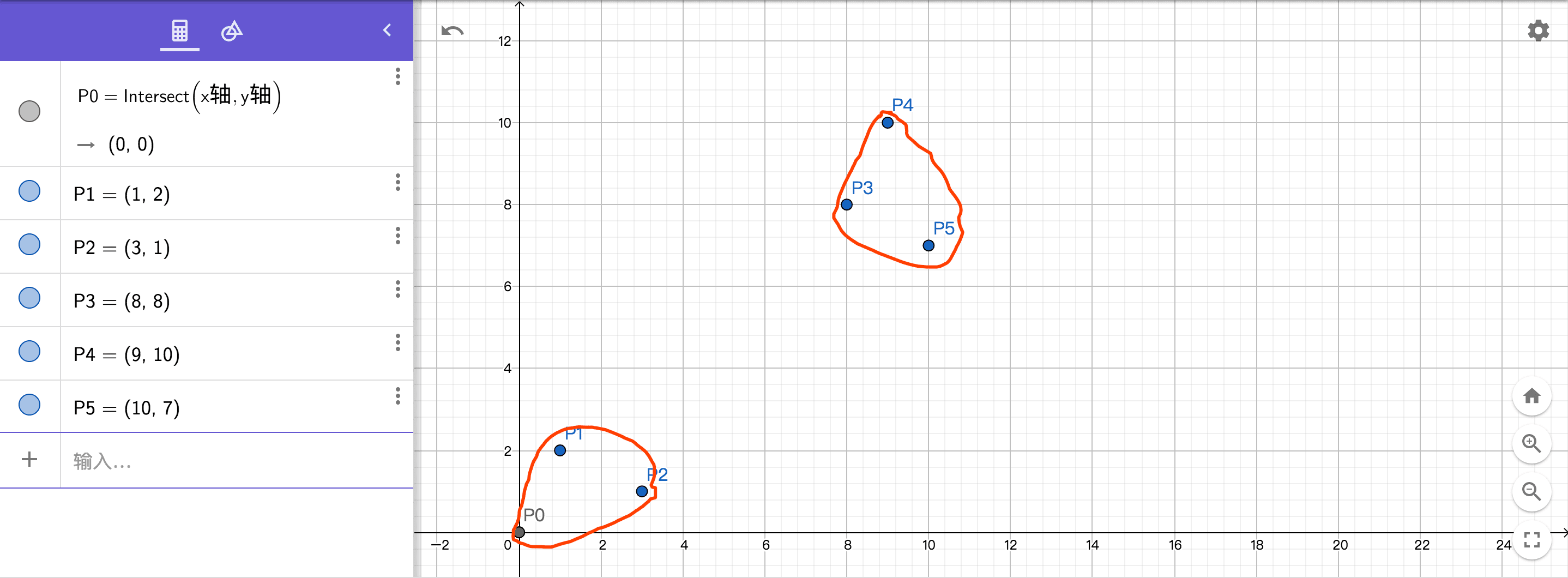
我们随便定义6个点P0、P1、P2、P3、P4、P5,在二维座标系中我们可以直观的看出,前面三个点在一堆,后面三个点在一堆。接下来我们通过 K-Means 算法验证一下是不是像我们实际看到的这种扎堆特征。
设定 K 值开始投票
我们定 K = 2,那么在6个点中随便选择两个点当作初始对象,这里我们就选 P0(0,0) 和 P1(1,2),接下来我们分别计算剩下4个点 P2、P3、P4、P5 和P0、P1的距离
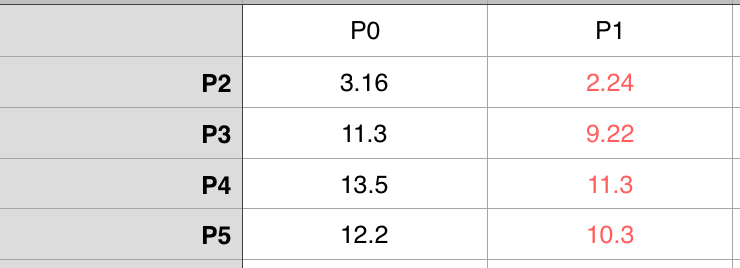
对比之后发现,在剩下的4个点中他们都和 P1 离的近一些,所以他们4个把票都投给了 P1,这时候就有两组 A 和 B,A={P0} ,B={P1,P2,P3,P4,P5}。
开始第二次投票
很显然 A 组只有 P0,所以 P0 这次还是初始对象,但是 B 组中现在有5个数据点,这次在 B 组中选取初始对象就不是随便选了,我们选择平均这5个点的横、纵坐标来形成一个之前没有的虚拟点位 P’ ,把P’当作 B 组的初始对象。那么 P’((1+3+8+9+10)/5,(2+1+8+10+7)/5) = (6.2,5.6)。这是新一轮投票结果
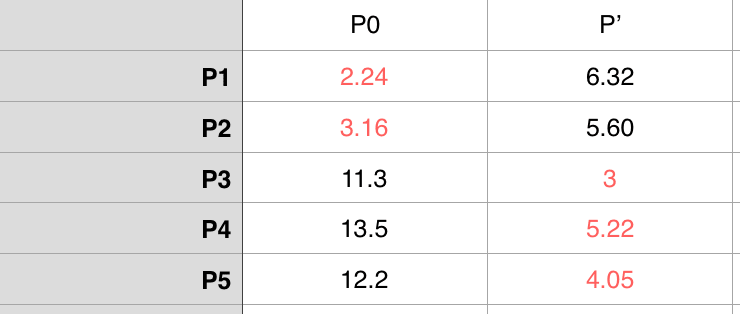
这次投票后形成的 A = {P0,P1,P2},B = {P3,P4,P5},这时候虚拟的数据点 P’ 就剔除。
再次投票
按照上面的逻辑和步骤,形成新一轮投票,这是两个新的初始点位分别是Pa’=(1.33,1),Pb’=(9,8.33),新的投票结果是

这次投票后 A = {P0,P1,P2},B = {P3,P4,P5},这和我们前面看到的”前面三个点扎堆,后面三个点扎堆”现象一致了。

我们可以发现,经过上面几次投票,数据已经出现了收敛,聚类到此结束,实验的结果和我们之前真实看到的完全一致。
