前言
前不久和华为安全团队聊到我们产品的加密算法,据华为内部最新安全规范,我们产品加密方式需要小面积做升级优化,我系统性的学习了一遍市场上常见的算法和底层逻辑。由衷的佩服数学的艺术,真的赞叹数学的神奇。也许生活中只有两种学问,一门是哲学,一门是数学。
加密类型
加密算法可以分为对称加密和非对称加密,对称加密在以前是非常常见的加密算法,随着应用和发展,后面逐步被非对称加密算法替代。
对称加密
我们举个例子说明此类加密的运行过程和逻辑。假设张三(下面简称Z)需要将一个信息A传递给李四(下面简称L),为了防止在传递过程中被截获窃听导致泄露,Z 需要将 A 做一道转化再传递给 L。比如 Z 这样操作 A-1=A’,将 A’传递给 L,L 拿到 A’ 后,再用 A’+1= A。我们看一下过程,即使在传递过程中 A’ 被截取窃听了,其实得到的也不是最原始的信息。我们把上述过程中 A 称之为明文,A’ 称之为密文,中间转化加的1称之为密钥,加1这个方式我们称之为加密算法。A’ 可以公开传递,秘钥部分是我们需要保密的,不能让其他非相关人员知道。

我们可以采用任何合理的方式得到 A’,比如乘以1,或者除以1,或者乘以100000等等,算法可以复杂到变态的程度。无论多么复杂的算法,L 最终得到 A 其实是做了和 Z 完全对称(逆向)的一个动作,你加1,我就在密文基础上减1,你乘以100000,我就开100000次根号。这种算法不管多么复杂,中间经过多少道运算,只要拥有足够多的密文,是可以通过穷举或者观察规律从而得到秘钥。于是就有人想到能不能每发一次密文就把秘钥换一个,做到动态分发秘钥?从上面简图看的出来,每更换一次秘钥,需要将这个秘钥准确安全的告诉 L,这个时候秘钥分发传递又成了一个问题(秘钥动态分发问题感兴趣可以查询资料,已得到解决)。
非对称加密
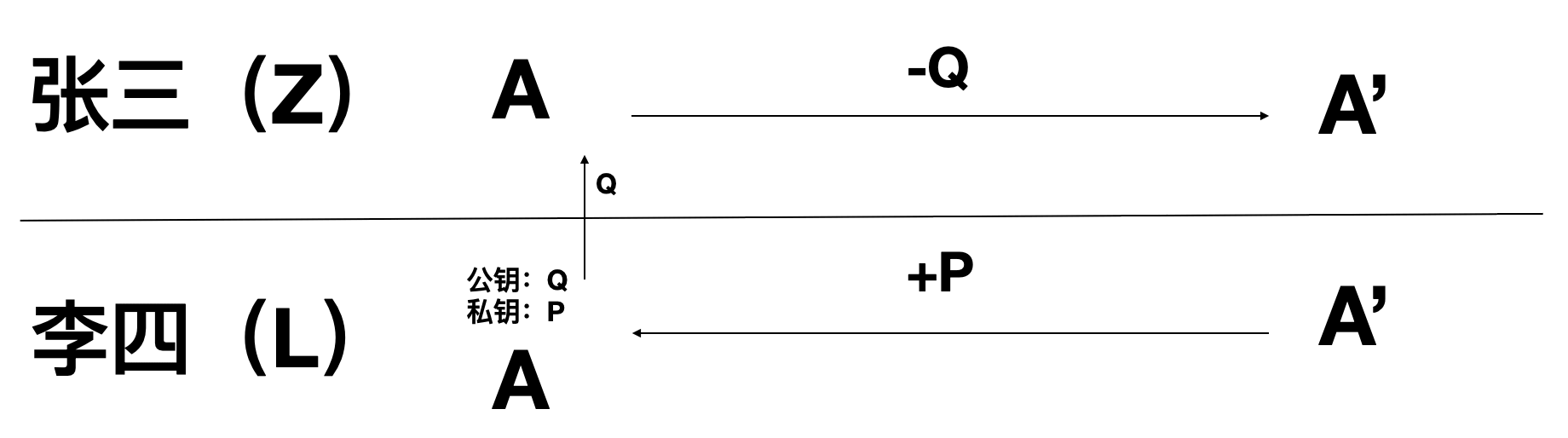
顾名思义,非对称加密就是 L 最终得到 A 不是简单的做了和 Z 完全对称的动作。还是上面的例子,Z 将 A 传递给 L,这个时候,L 会先生成一对公私钥 Q 和 P,在 Z 传递密文之前,L 先把公钥 Q 传递给 Z,Z 拿到 Q 之后,将 A-Q =A’ 传递给 L,L 拿到 A’ 之后不是简单的 A’+Q 而是 A’+P=A。整个过程不对称的地方就在这里,加密时候是减去公钥 Q,解密时候加上私钥 P。Q 和 P 之间的关联关系能够使得L 最终做 A’+P 这个动作得到明文 A。
RSA 算法
1977年在麻省理工学院工作的罗纳德•李维斯特(Ron Rivest)、阿迪•萨莫尔(Adi Shamir)和伦纳德•阿德曼(Leonard Adleman)提出了一种非对称加密算法,算法名字就取三位教授的姓氏首字母R、S、A;此算法后面被广泛应用,下面一起看一下 RSA 的工作原理。
还是上面的例子,Z 将 A 传递给 L,为了顺利的进行,L 需要做些准备工作:
1、L 先找到两个质数。假设找到的为 V 和 W
2、做一道运算,得到一个数字X。运算方式为 X=V•W
3、取一个函数 F(X)。令 F(X)=(V-1)(W-1)
4、找出一组公私钥 Q 和 P。使得 Q 满足:1<Q<F(X) 且 Q 和 F(X)是互质关系。使得 P 满足:Q•P除以 F (X)得到的余数为1。找出这样一组数字并不难,比喻Q=3,P=11,F(X)=32
有了上面的准备工作,接下来看看实际的加密过程,Z 加密过程会做:
1、首先将明文 A 做一道运算,计算 A 的 Q 次幂得到 A1
2、再将 A1 除以 X 得到余数 A’,A’ 就是密文
3、Z 将 A’ 传递给 L
加密过程做完之后,L 将就行解密,L 做以下事情:
1、首先对密文 A’ 做一道运算,计算 A’ 的 P 次幂得到 A2
2、再将 A2 除以 X 得到余数(暂定为Y)
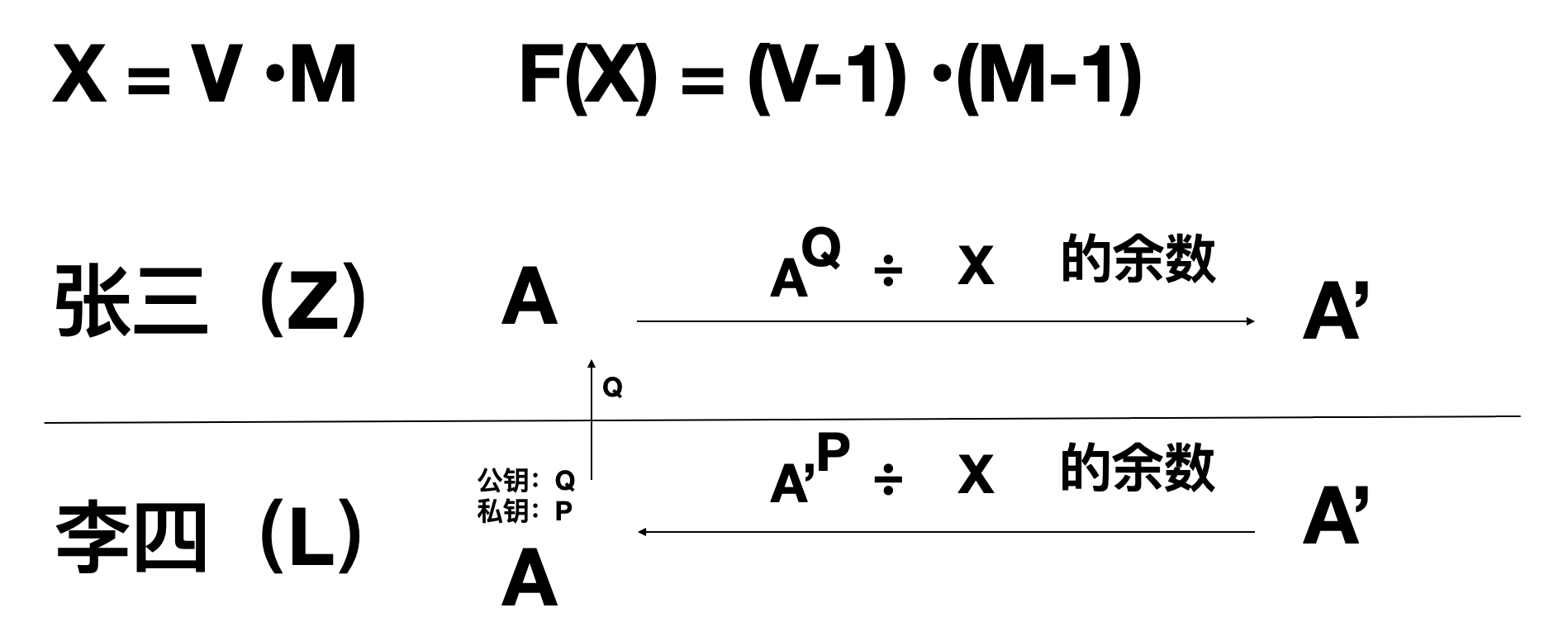
经过上面一系列的数学运算,似乎得到的 Y 和 A 没有任何联系,实际能够从数学上证明最终 L 解密得到的 Y 就是最初明文 A。看到这里,除了惊讶数学的神奇,更多的是敬仰数学的艺术性。
安全传递
RSA 算法中,
加密过程公开传递的参数:公钥 Q、质数乘积 X 以及密文 A’
解密过程需要的参数有私钥 P、质数乘积 X 和密文 A’
假设某一个人窃听了公开传递的参数 Q、X、A’,他想得到 P、X、A’,就必须先求出 P,看一下上面第4步中 Q 和 P 的关系是 Q•P 除以 F(X) 余1,那要想通过 Q 求出 P,先得求出 F(X),而 F(X) = (V-1)(W-1),所以想要求出 F(X) 得先求出 V 和 W,从上面第2步可以得知 X = V•W,问题转化为:已知 X,想要求出 V 和 W。到这里应该已经发现了,这其实就是质因数分解。如果 X 很简单,比如 X =21,那 {Q=3,P=7}就是一组,但是如果 X 是一个1024位数字,这种大数质因数分解,目前人类是无法做到的,用两个足够大的质数相乘得到一个1024位的数字可以做到,但是给你一个1024位的数字,让你分解出两个质数,人类的算力目前无法完成。

最后
普通计算机的计算能力某些场合已经超过人类,量子计算机的算力能力是普通计算机的数十倍。每隔一段时间,银行或者身边常见的 App 都会提示你更新密码或者证书,这其实就是在规避被强力破解的风险;生活中没有绝对的安全,所谓的安全无非是中间的信息差暂时不会大面积公众。
